Graphing Polynomial Functions Worksheets⁚ A Comprehensive Guide
This guide provides a thorough exploration of graphing polynomial functions, encompassing worksheets with detailed solutions․ Master key concepts, from identifying zeros and multiplicities to determining end behavior and sketching accurate graphs․ Practice exercises and real-world applications are included for a comprehensive understanding․
Understanding Polynomial Functions
Polynomial functions are fundamental algebraic expressions forming the bedrock of many mathematical concepts․ They consist of terms involving variables raised to non-negative integer powers, each multiplied by a constant coefficient․ The highest power of the variable determines the degree of the polynomial, significantly influencing its graph’s shape and behavior․ For instance, a linear function (degree 1) produces a straight line, while a quadratic function (degree 2) results in a parabola․ Higher-degree polynomials exhibit more complex curves, with the number of potential turning points related to the degree․ Understanding the structure of polynomial functions – the coefficients, variables, and exponents – is crucial for predicting their graphical representations․ Worksheets often begin by reinforcing this foundational knowledge before progressing to more advanced graphing techniques․ A solid grasp of polynomial definitions and their components is essential for interpreting and creating accurate graphs․
These functions are expressed in the general form⁚ f(x) = anxn + an-1xn-1 + ․․․ + a1x + a0, where ‘a’ represents the coefficients, ‘x’ the variable, and ‘n’ the degree (a non-negative integer)․ The constant term, a0, is the y-intercept where the graph crosses the y-axis․ Analyzing these elements is crucial in understanding the behavior and characteristics of the polynomial’s graph․
Identifying Zeros and Multiplicities
A crucial step in graphing polynomial functions involves pinpointing the zeros, also known as roots or x-intercepts․ These are the values of x where the function’s value, f(x), equals zero; graphically, these are the points where the curve intersects the x-axis․ Locating these zeros is often the starting point for many graphing exercises․ Factoring the polynomial expression is a common method for finding zeros; each factor corresponds to a zero․ However, some polynomials may require more advanced techniques, such as the use of the quadratic formula or numerical methods․ The multiplicity of a zero indicates how many times a particular zero appears as a root of the polynomial․ This multiplicity impacts the graph’s behavior at that specific x-intercept․
A zero with an odd multiplicity (e․g․, 1, 3, 5) causes the graph to cross the x-axis at that point․ In contrast, a zero with an even multiplicity (e;g․, 2, 4, 6) results in the graph touching the x-axis but not crossing it – it “bounces” off the axis at that point․ Worksheets often include exercises focusing on identifying zeros and their multiplicities from either the factored form of the polynomial or its graph․ This understanding is essential for accurately sketching the polynomial curve and for understanding its overall behavior․ Recognizing the relationship between a zero’s multiplicity and the graph’s behavior near the x-intercept is fundamental to accurate graphing․
Determining End Behavior
Understanding the end behavior of a polynomial function is crucial for accurately sketching its graph․ End behavior describes how the function’s values behave as x approaches positive or negative infinity․ The degree of the polynomial and the sign of its leading coefficient are the key determinants of end behavior․ The degree, or highest power of x in the polynomial, dictates the overall shape of the graph․ For polynomials of odd degree, the graph extends in opposite directions as x approaches infinity and negative infinity․ In contrast, even-degree polynomials have both ends pointing in the same direction․
The leading coefficient, the numerical coefficient of the term with the highest power of x, determines the direction of the ends․ A positive leading coefficient results in the graph rising as x approaches positive infinity․ Conversely, a negative leading coefficient causes the graph to fall as x approaches positive infinity․ Worksheets often include exercises that require students to determine a polynomial’s end behavior based solely on its degree and leading coefficient, without needing to graph the entire function․ This understanding is crucial for quickly assessing the general shape and direction of the graph, providing valuable insight before more detailed analysis is performed․ Mastering this skill significantly improves the efficiency and accuracy of graphing polynomials․
Sketching Polynomial Graphs
Sketching polynomial graphs effectively involves a systematic approach incorporating several key elements․ Begin by identifying the polynomial’s zeros (x-intercepts) and their multiplicities․ The multiplicity of a zero indicates whether the graph crosses or touches the x-axis at that point․ A multiplicity of 1 results in a cross, while even multiplicities cause the graph to touch and turn․ Next, determine the y-intercept by evaluating the function at x=0․ Understanding the end behavior, as discussed previously, provides valuable information regarding the graph’s overall direction at its extremes․ Combining this knowledge of intercepts and end behavior helps to establish a framework for sketching the graph․
Consider the polynomial’s degree; this determines the maximum number of turning points (local maxima or minima) the graph can possess․ While not all turning points are always present, this information guides expectations about the graph’s shape and complexity․ Remember to plot additional points, if necessary, to refine the sketch and ensure accuracy․ These points can help clarify the graph’s behavior between the zeros and accurately depict the curve’s shape․ Practice worksheets often include examples of varying degrees and complexities, allowing students to develop their proficiency in graphing polynomials․ Accurate sketching requires a solid understanding of these concepts and a systematic approach․
Finding x-intercepts and y-intercepts
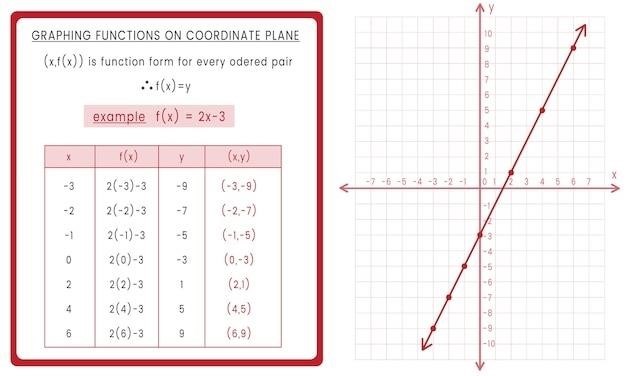
The x-intercepts of a polynomial function represent the points where the graph intersects the x-axis, meaning the y-coordinate is zero․ To find these intercepts, set the polynomial function equal to zero and solve for x․ Factoring the polynomial is often the most efficient method, yielding the x-values where the graph crosses or touches the x-axis․ Each solution corresponds to an x-intercept․ The multiplicity of a root influences the behavior of the graph at that intercept; a multiplicity of 1 results in a simple crossing, while even multiplicities cause the graph to touch and turn․ Understanding multiplicities is crucial for accurately sketching the graph․
In contrast, the y-intercept is the point where the graph intersects the y-axis, meaning the x-coordinate is zero․ Finding the y-intercept is straightforward; simply substitute x = 0 into the polynomial function and solve for y․ The result is the y-coordinate of the y-intercept, typically written as the ordered pair (0, y)․ This point provides a crucial anchor point for sketching the graph, especially when combined with information about the x-intercepts and end behavior․ Worksheets on graphing polynomials frequently emphasize the importance of accurately determining both x- and y-intercepts as essential steps in the graphing process․
Working Backwards⁚ Finding Polynomial Functions from Graphs
A valuable skill in understanding polynomial functions involves working backward from a given graph to determine the corresponding polynomial equation․ This process enhances comprehension of the relationship between a function’s characteristics and its graphical representation․ Begin by identifying the x-intercepts of the graph, as these directly correspond to the roots of the polynomial․ The x-coordinate of each intercept represents a root, and its multiplicity can be determined by observing the graph’s behavior at that point․ A simple crossing indicates a root with multiplicity 1, while a touch and turn suggests an even multiplicity․
Once the roots and their multiplicities are established, construct the factored form of the polynomial․ Each root ‘r’ with multiplicity ‘m’ contributes a factor (x ─ r)^m․ Multiply these factors together to obtain a polynomial in factored form․ Note that this process may not produce the exact polynomial equation if the graph does not provide sufficient information, such as the leading coefficient․ A leading coefficient can often be determined by analyzing the graph’s end behavior and using a known point on the graph to solve for any remaining unknown constants․ Remember, this reverse-engineering approach strengthens your understanding of polynomial functions’ visual and algebraic representations, and is a common component of many graphing polynomial worksheets․
Real-World Applications of Polynomial Functions
Polynomial functions, while seemingly abstract, possess significant real-world applications across diverse fields․ In engineering, they model the trajectory of projectiles, crucial for designing accurate missile systems or predicting the flight path of aircraft․ The study of polynomial functions is also central to designing roller coasters, ensuring a thrilling yet safe ride․ Careful modeling is critical to ensure the coaster smoothly navigates curves and hills while remaining within safety parameters․
Beyond engineering, polynomial functions find utility in economics․ They can model cost functions, allowing businesses to optimize production and pricing strategies․ By understanding the cost function’s shape and behavior, companies can determine the most profitable production levels․ Furthermore, polynomial functions are essential in financial modeling, helping to predict market trends and assess investment risks․ The ability to analyze and interpret polynomial graphs is paramount in making informed decisions in these areas․ Worksheets focused on graphing these functions provide the necessary foundational skills for tackling these real-world applications, bridging the gap between theoretical concepts and practical problem-solving․
Solving Polynomial Inequalities
Solving polynomial inequalities builds upon the foundational understanding of graphing polynomial functions․ The process leverages the graphical representation to identify intervals where the function’s value is positive or negative, directly corresponding to the solution of the inequality․ By locating the x-intercepts (zeros) of the polynomial, we can partition the number line into intervals․ Testing a value within each interval determines whether the polynomial is positive or negative in that region․
This approach efficiently determines the solution set of the inequality․ Consider an inequality like f(x) > 0․ The solution set comprises all x-values where the graph of f(x) lies above the x-axis․ Conversely, for f(x) < 0, the solution set includes x-values where the graph is below the x-axis․ Worksheets designed for practice typically include a mix of inequalities requiring both graphical analysis and algebraic manipulation, reinforcing the connection between the visual representation and the algebraic solution․ This dual approach ensures a comprehensive understanding of solving polynomial inequalities․
Additional Resources and Practice Problems
To further enhance your understanding and skills in graphing polynomial functions, various resources are readily available․ Online platforms offer interactive exercises and tutorials, providing immediate feedback and reinforcing concepts․ Many websites provide downloadable worksheets with varying difficulty levels, allowing for targeted practice based on individual needs․ These worksheets often include comprehensive answer keys, enabling self-assessment and identification of areas needing further attention․
Textbooks dedicated to precalculus or algebra often contain dedicated sections on polynomial functions, providing detailed explanations and numerous practice problems․ These resources frequently incorporate real-world applications, illustrating the relevance of polynomial functions in diverse fields․ Furthermore, seeking assistance from teachers or tutors can provide personalized guidance and address specific challenges․ Remember that consistent practice is key to mastering graphing polynomial functions; regular engagement with diverse problems and resources will solidify your understanding and improve your problem-solving skills․